

![]()
The complex trace consists of a real trace, which is identical to the input stack trace, and an imaginary trace, which is the Hilbert transform of the real, stacked seismic trace. Consequently, the Hilbert transform is the key process in the calculation of a complex seismic trace.
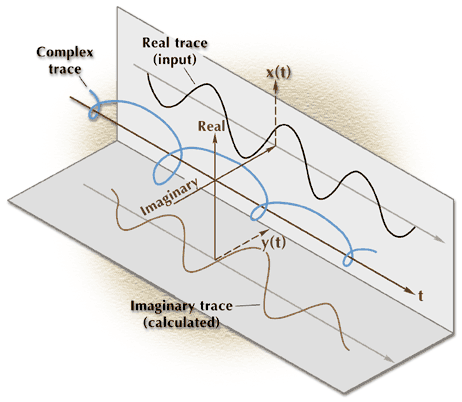
Figure 1. The complex seismic trace consists of a real component, the actual recorded seismic trace, and an imaginary component which is calculated via the Hilbert Transform. In a 3-dimensional plot, the real and imaginary components combine to produce a helical appearing function that spirals about the time axis.
The Hilbert transform
is basically a special kind of filter which shifts all positive frequencies
of an input signal by -90 degrees and all negative frequencies by +90 degrees.
If x (t) is the input signal, y (t) is the output, and G (![]() )
is the Hilbert transform filter expressed in the frequency domain, then the
Hilbert transform process can be expressed mathematically as
)
is the Hilbert transform filter expressed in the frequency domain, then the
Hilbert transform process can be expressed mathematically as
![]()
where H (x
(t)) is the Hilbert transform of x (t), j = ![]() and sgn (
and sgn (![]() ) is defined as
) is defined as
![]()
There are certain requirements on the input signal, x (t), which are necessary before a valid Hilbert transform can be calculated, such as,
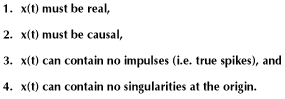
A stacked seismic trace satisfies all of these prerequisites so it is a valid candidate for the Hilbert transform process. For a stacked seismic trace, or any valid input x (t), the Hilbert transform, H (x (t)), has the following properties:
 |
 |
| ©1999 AGI |