

Various terminology exists in the scientific literature for the mathematical elements of the Hilbert transform and for the data manipulations that it performs, and this variety of descriptive terms is the source of some confusion. The differing terminology results because the Hilbert transform is used in several scientific disciplines, including mathematics, electrical engineering, and geophysics, and each of these groups has coined terms to describe the calculation process. Some common definitions associated with the Hilbert transform are illustrated in Figure 2.
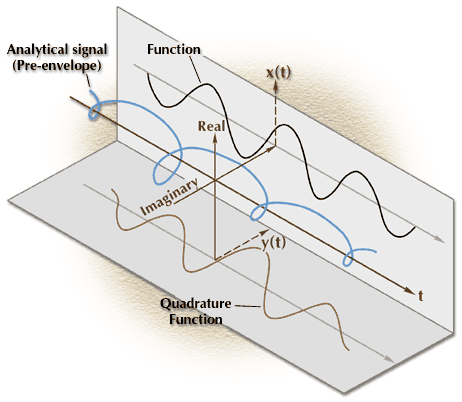
Figure 2. Some of the terminology used to describe the Hilbert transform process is labeled here and can be compared to the terminology used by geophysicists which is shown in Figure 1.
The mathematician's term "analytic signal" and the electrical engineer's term "pre-envelope" are synonymous with the geophysicist's "complex seismic trace". The mathematician's "quadrature function", y (t), is the Hilbert transform of the real input "function", x (t), and represents the imaginary part of the analytic signal. In geophysical terms, x (t) is the stacked seismic trace, and y (t) is the Hilbert transform of the stacked trace. Both x (t) and y (t) are real quantities (Property 1), but the two terms can be combined into the complex seismic trace represented by the helical curve in Figure 1 whose projections on the real and imaginary planes are x (t) and y (t), respectively.
A Numerical Technique for Constructing the Complex Seismic Trace
The complex seismic trace, z (t), of a real, causal, stacked seismic trace, x (t), is defined as
![]()
where y (t)
is the Hilbert transform of x (t). The mathematical development of the complex
trace is probably best done in the frequency domain. Let X (![]() ),
Y(
),
Y(![]() ), and Z(
), and Z(![]() )
be the Fourier transforms of x (t), y (t), and z (t), then Equation 3 can
be written as
)
be the Fourier transforms of x (t), y (t), and z (t), then Equation 3 can
be written as
![]()
From Equations 1 and 2,
![]()
so that Z
(![]() ) can be simplified to
) can be simplified to
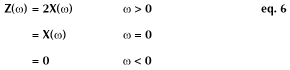
 |
 |
| ©1999 AGI |