
|

|
| ©2000 AGI |

Net-Pay Cutoff
The two most critical issues in the determination of net pay are permeability
to reservoir fluids and water saturation. In many cases analysts use
other criteria for net pay, such as porosity and shale volume. Although
porosity is an important input in the net-pay determination process,
if the researcher has a good permeability model, a separate porosity
criterion is unnecessary. In many cases the use of a porosity criterion
alone for net pay can lead to erroneous calculations of net pay because
permeability is a function of both porosity and irreducible water saturation.
If the irreducible Bulk Volume Water (BVW) (the product of porosity
and water saturation) is not a constant value within the reservoir,
the porosity-permeability relationship will not be consistent either.
High irreducible BVW zones require higher porosity values to achieve the same permeability as lower porosity low irreducible BVW zones. Clay volume is an input to the process as well, refining both porosity and water saturation calculations. It is unnecessary to have clay volume as a separate net-pay criterion after permeability and Sw models have been calibrated.
Permeability
to Reservoir Fluids
Permeability is the ability of fluids to move in the reservoir. The
net-pay cutoff should be based on how effective permeability is to reservoir
fluids under reservoir conditions. Most core permeability data concern
air-at-surface conditions, and adjustments should be made to these values
to reflect in situ conditions. In dry gas reservoirs, reasonable estimates
can be obtained from core data analyzed under net overburden stress
conditions using Klinkenberg corrections. This type of analysis is not
generally cost prohibitive, and not all samples need it.
Excellent correlations can commonly be obtained on a subset of the total core data set that allows the net overburden Klinkenberg corrections to be applied to all samples. Correlations can also be done in oil reservoirs; however, significantly more expense and effort are required. Determining the values of effective permeability to oil and water is a useful exercise. Part of this effective-permeability determination process is estimating irreducible water saturation and relative permeability to oil and water. These issues will be discussed in the next section. In the absence of special core analysis in oil zones, a reasonable calibration can be made to pressure transient data. In this case it is important to use the value of permeability-thickness from the well test and to match the log-derived permeability thickness, rather than the assumed permeability value. The permeability value from a well test requires an input of net pay that may or may not be valid before proper calibration.
Factors Affecting
the Permeability Cutoff
Type of completion is an issue because lower permeability zones having
hydraulic fractures can be economically produced, whereas identical
zones having no stimulation may not be. Many of the low-permeability
gas zones in the U.S. had little or no net pay before hydraulic fracturing
was introduced, although today these same reservoirs are responsible
for a good deal of the total gas produced. If the zone cannot be stimulated,
the amount of skin damage expected becomes a factor. Lower permeability
zones that can be drilled without skin (using techniques such as underbalanced
drilling) can be economically produced, whereas equivalent permeability
zones with high skin damage may not. In the case of hydrocarbon zones
close to water zones, one zone may contain net pay if sufficient stress
contrast exists between the hydrocarbons and the water, although an
identical zone may not be considered net pay because a hydraulic fracture
would result in uneconomic water production. The viscosity of the produced
fluid is also an issue, gas reservoirs requiring permeabilities to produce
economically that are significantly lower than those of oil reservoirs.
Reservoir pressures and flowing well-bore pressures are also an issue.
Zones having high reservoir pressures and high drawdowns can be produced
economically at lower permeabilities than can lower pressure and drawdown
zones having equivalent permeabilities. All of these factors go into
the permeability cutoff for net-pay determination. A detailed discussion
of these is beyond the scope of this exercise, and it is assumed here
that this value has been determined by the reservoir engineer and petrophysicist
for the field. If additional background is needed for establishing permeability
and Sw criteria for net pay, a review of the references is recommended.
Water Saturation
Water saturation (Sw) is the second key parameter that must be estimated
to determine net pay. Three water saturation values need to be specified
to determine net pay adequately. The first is irreducible water saturation
for the formation, or Swirr, which is the water bound by capillary forces
to the matrix that will not move. The second is water saturation in
the reservoir at the time the well logs were obtained, or Sw. If Sw
is equal to the irreducible Sw, then the zone should produce no water.
As Sw increases above Swirr, higher and higher water cuts can be expected.
At some point the third Sw value (Swcritical) is reached, where the
water cut is unacceptable. This impacts net pay determination is the
Sw where water cuts become uneconomic. Because the SPE definition of
reserves includes an economic caveat, factors such as water-disposal
costs and lifting costs enter into the equation. The current Sw is generally
calculated from log data once the Sw model has been calibrated to irreducible
Sw data. The Swirr can be obtained from core capillary-pressure data
and from core-calibrated Nuclear Magnetic Resonance (NMR) log data.
The NMR log should have a calibrated T2 value to discriminate mobile
and nonmobile fluids because the default value of 33 ms does not apply
to all reservoirs. Swcritical can be obtained from core relative-permeability
data and fractional flow calculations if available. A more commonly
used technique is to compare Sw values from the logs with actual water
cuts in the field. Once the Sw model is calibrated to Swirr from core
capillary-pressure data or NMR log data, the Sw in the reservoir that
results in uneconomic produced water cuts is probably a reasonable first
estimate of the critical Sw value in the absence of relative permeability
and fractional flow data from cores. This Sw value is typically in the
50- to 70-percent range in most light oil and gas reservoirs where high
water cuts are unacceptable, the lower Sw critical values usually being
associated with higher permeability rocks. The value is also a function
of viscosity, for heavy-oil values as low as 25 to 30 percent Sw have
resulted in uneconomic water cuts.
Intermediate Steps to Calculating Water Saturation and Effective Permeability
The basic inputs to calculating water saturation and effective permeability are shale volume, apparent porosity, and resistivity. Shale volume will be used to convert apparent porosity to an effective porosity value. It will also be used to correct the resistivity value for the effect of shale. A discussion of these three parameters is in order.
Shale Volume
The volume of shale or clay in the rock can be determined from gamma-ray
(GR), spontaneous-potential (Sp), resistivity, neutron, neutron and
density, sonic, or NMR data. In some cases a combination of indicators
is required where either the minimum or a specialized average is used.
In the exercise provided it is assumed that gamma ray will be used.
A discussion of other techniques can be found in Asquith.
The basic process is to determine a value of the tool measurement that
corresponds to sand and a value that corresponds to shale. The percentage
of shale is determined by finding the difference between the actual
value and the clean value divided by the total difference between the
sand and shale values. In the case of the more commonly used gamma ray,
there is not a linear relationship as the equation provided in the exercise
indicates. The key calibration value for the volume of shale is the
X-Ray Diffraction technique (XRD). This technique measures the bulk
volume of shale as a percentage of total rock volume. The Scanning Electron
Microscope technique also provides a clay volume by a direct examination
of core slices. It is not recommended for the calibration of log-based
shale volume if XRD data are available.
Apparent Porosity and Effective Porosity
The next key input
to calculating effective permeability and net pay is apparent porosity.
Apparent porosity is the raw porosity input with no shale corrections.
In most cases this value is obtained from the average of neutron and
density porosity values or the square root of the average of the values
squared for gas wells. Density porosity alone can often be used, as
it is in the exercise in this module. Sonic porosity can also be used,
as can neutron or MRIL data. In the case where no porosity logs are
available, a correlation can often be obtained in fluvial-deltaic systems
between an assumed value of maximum porosity as a function of depth
and as a function of shale volume. This correlation has been successfully
applied in the Miocene in several reservoir characterization studies.
Once the apparent porosity value is determined, it should be corrected
for shale volume. There are two main techniques applied here. The first
quick-look technique is to reduce the apparent porosity by the percentage
of shale in the rock or multiply it by one minus the shale percentage.
A more technically correct method is to estimate the porosity in the
shales and reduce the apparent porosity by the product of the shale
porosity and shale volume. This is the technique applied in the exercise.
Asquith provides an excellent discussion of the techniques and equations
involved.
The net-pay criteria are established by the reservoir engineer and petrophysicist. In this exercise, they have calibrated the log-analysis model to core and determined that permeabilities over 0.001 md will provide economic flow rates. Figure 1 (below) shows a log calibration to core, and in this case there is reasonable agreement between core-calculated values and log calculations. They have also determined that water saturations over 60 percent will result in uneconomic water-production volumes. Other necessary information for determining net pay includes bulk density, gamma ray, caliper, and resistivity. The equations necessary to determine whether each of the provided samples presented qualifies as net pay can be found in the glossary. Ultimately this determination will require a calculation of effective porosity, water saturation, and permeability to gas. All of the steps leading up to these calculations must be done first.
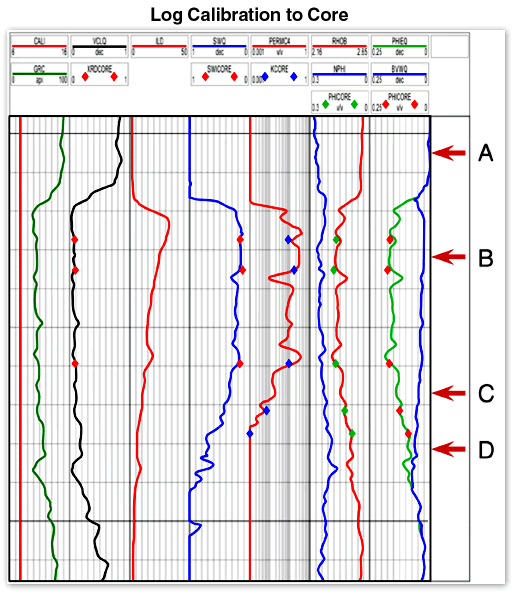
Figure 1. Log calibration to core ; log-derived values of PHIE, Sw, Vshale; and permeability agree reasonably well with core data.
Below is a flow chart for calculating GR shale volume (figure 2). The
process includes correcting the raw gamma-ray data for hole size and
mud weight, then estimating shale volume from the corrected gamma ray.
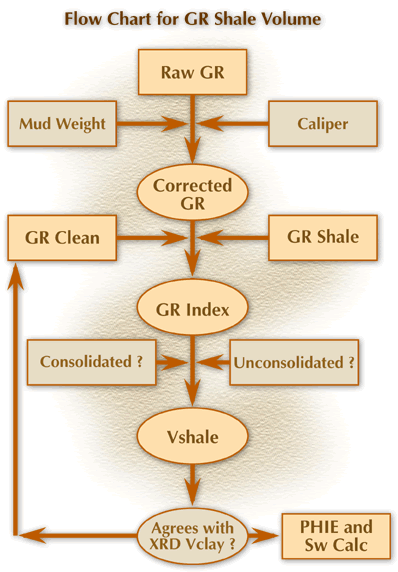
Figure
2.
USE OF GR PICKS AND XRD VALUES
The GR picks chosen
are used for a first estimate when actual, measured, clay-volume data
are available. Comparison of the XRD values with the GR-derived values
indicated a clean value of 30 and a shale value of 101.
In this case, the clean value of 30 should be slightly lower than the
pick from the log because these zones are not 100 percent sandstone.
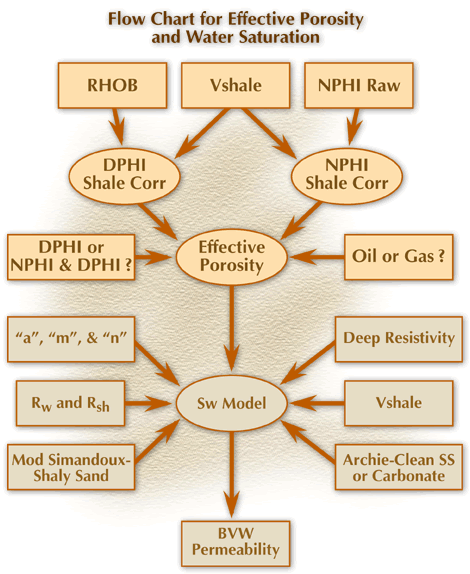
Figure 3. Flow chart for effective porosity and water saturation , correcting porosity inputs for clay volume, calculating Sw from porosity, Vshale, and resistivity inputs, and estimating permeability.
Simandoux
water saturation equation
There are several good techniques available for estimating the effect of shale resistivity water saturation. The Simandoux water saturation equation is used here. It is fairly complex; however, it can be easily calculated using a spreadsheet.
Here is a modified version of the Simandoux Equation:
Sw=(0.5*Rw/PHIE^m)*((4* PHIE^m)/(Rw*ILD)+(Vclay/Rshale)^2)^(1/n)-Vclay/Rshale)
where:
m=2.08, n=1.44, Y Rshale=1.8 ohm-m
Calculating Permeability
from Logs
A number of algorithms have been published that estimate permeability
from well log data. The model that is recommended is the modified Coates-Denoo
technique, which has a variable correlation factor that allows for correlation
to real data. It requires inputs of effective porosity and Bulk Volume
Water Irreducible (BVWirr). The concept of BVWirr is relatively simple
yet very powerful in the estimation of permeability. It is the product
of irreducible water saturation and effective porosity, and it represents
the volume of the rock that is filled with immobile fluids. It compares
to Sw in that Sw is the percent of the effective porosity that is water
filled. The nuclear magnetic resonance log is useful in this process
because it provides a direct measurement of BVWirr once the T2 cutoff
has been calibrated to core data. The calculated permeability from NMR
logs should be used with caution, however, because it requires calibration
to real data prior to use as a permeability tool. If this calibration
has not been done, it is recommended that the modified Coates-Denoo
technique be used with only the input of BVWirr from the NMR tool.
The following flow chart (figure 4) illustrates a general process for arriving at a calibrated permeability.
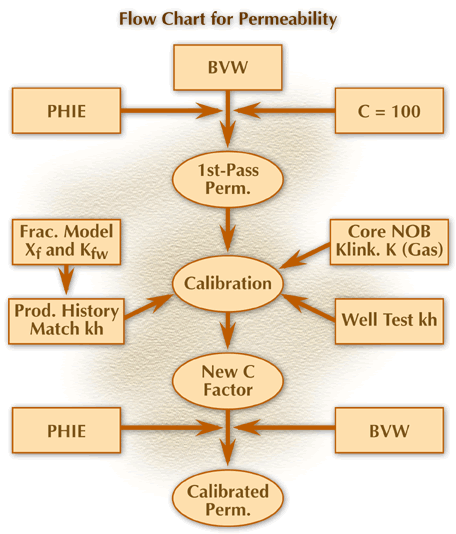
Figure 4