The dominant wavelength associated with a seismic wavelet is defined as the distance between two identical phase points of an oscillating function, as shown in Figure 1 below.

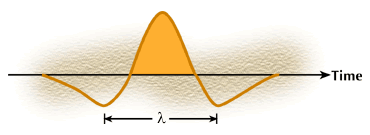
Figure 1. Definition of dominant wavelength. Wavelength is the distance between two identical phase points on an oscillating function. Typically wavelength is measured between adjacent peaks or troughs as shown by the symbol above. This seismic wavelet contains a wide spectrum of wavelengths, but the wavelength that is most apparent is the one shown by , this it is called the dominant wavelength.

Typically, wavelength is measured between adjacent peaks or troughs by the symbol l. This seismic wavelet contains a wide spectrum of wavelengths, but the wavelength that is most apparent is the one shown by ; thus it is called the dominant wavelength.

A thin bed is a stratigraphic unit that has a thickness much less than the dominant wavelength of the seismic wavelet that illuminates the bed. It is generally accepted that if is the dominant wavelength of the illuminating seismic wavelet, then a thin bed is a bed with a thickness that is one-fourth of or less. It is important to note that the definition of a thin bed depends on the length of the investigative wavelength. A bed that is thin relative to a low-frequency (long-wavelength) wavelet may not be thin when a higher frequency (shorter wavelength) wavelet is considered, as is illustrated in the following figure.

Figure 2. Relationship between dominant wavelength and seismic thin beds. Thin beds are units that have thicknesses that do not exceed one-fourth of the dominant wavelength. A reservoir that is a thin bed when illuminated by a low-frequency wavelet (right) may not be a thin bed when illuminated by a high-frequency wavelet (left)