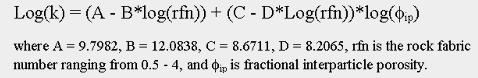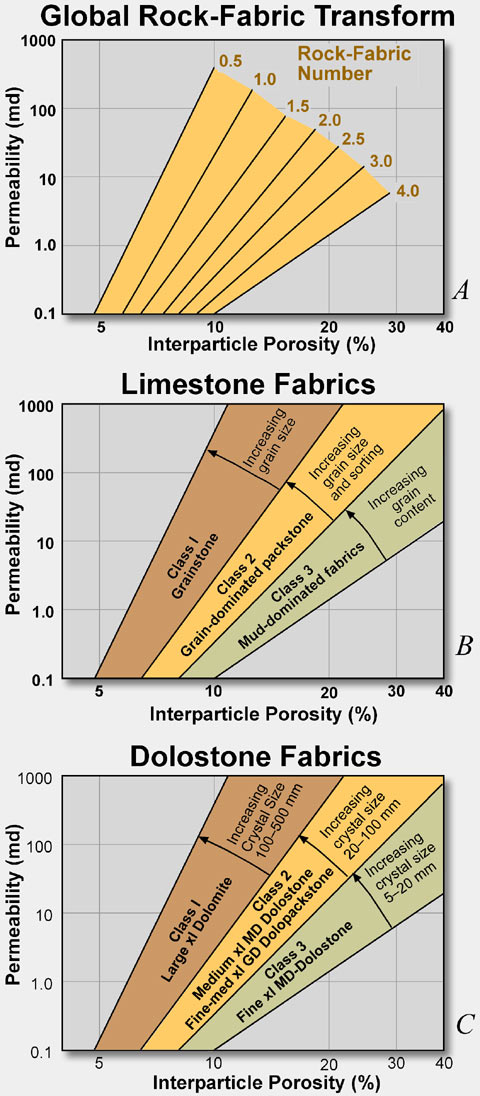
Rock-Fabric/Petrophysical Relationships

Petrophysics of Interparticle Pore Space

Global Interparticle-porosity Permeability Transform

Although fabrics are divided into three petrophysical classes, in nature there is no boundary between the classes. Instead, there is a continuum from mudstone to grainstone and from 5 to over 500 mud-dominated dolostones (Fig. 14b,c). Therefore, there is also a complete continuum of rock-fabric specific porosity-permeability transforms.

Figure 14. Continuum of rock fabrics and associated porosity-permeability transforms. (A) Rock-fabric numbers ranging from 0.5 - 4 defined by class-average and class-boundary porosity-permeability transforms. (B) Fabric continuum in nonvuggy limestone. (C) Fabric continuum in nonvuggy dolostone.

To model such a continuum the boundaries of each petrophysical class are assigned a value (0.5, 1.5, 2.5, and 4) (Fig. 14a) and porosity-permeability transforms generated. These transforms were added to the class 1, 2, and 3, transforms and an equation relating permeability to a continuum of class values and interparticle porosity is developed using multiple linear regressions. To avoid confusion, the class values generated by this equation are termed rock-fabric numbers. The resulting global transform is given below. This equation is useful in calculating permeability from wireline logs but is too detailed to be useful for routine classification of visual descriptions.

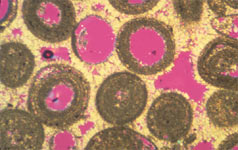
Mud-dominated limestones and fine crystalline mud-dominated dolostones occupy rock fabric numbers from 4 to 2.5 (Fig. 14b,c). The class number decreases with increasing dolomite crystal size from 5 to 20 in mud-dominated dolostones, and with increasing grain volume in mud-dominated limestones. Grain-dominated packstones, fine-to-medium crystalline grain-dominated dolopackstones, and medium crystalline mud-dominated dolostones occupy the rock fabric numbers from 2.5 to 1.5 (Fig. 14b,c). The class value decreases with increasing dolomite crystal size from 20 to 100 in mud-dominated dolostones and with decreasing amounts of intergrain micrite as well as increasing grain size in grain-dominated pack-stones and fine to medium crystalline grain-dominated dolopackstones. Grain-stones, dolograinstones, and large crystalline dolomites occupy rock fabric numbers 1.5 to 0.5 (Fig. 14b,c). 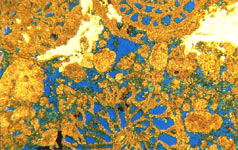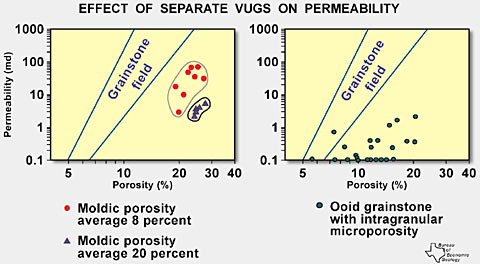The class value decreases with increasing grain size and dolomite crystal size from 100 to 500.

Unusual Types of Interparticle Porosity

Diagenesis can produce unique types of interparticle porosity. Collapse of separate-vug fabrics due to overburden pressure can produce fragments that are properly considered "diagenetic particles". Large dolomite crystals with their centers dissolved can collapse to form pockets of dolomite rims. Leached grain-stones can collapse to form intergrain fabrics composed of fragments of dissolved grains. These unusual pore types typically do not cover an extensive area. However, the collapse of extensive cavern systems can produce bodies of collapse breccia that are extensive. Interbreccia-block pores produced by cavern collapse are included in the touching-vug category because they result from the karsting process (Kerans 1989).

Petrophysics of Separate-Vug Pore Space

The addition of separate-vug porosity to interparticle porosity alters the petrophysical characteristics by altering the manner in which the pore space is connected, all pore space being connected in some fashion. Examples of separate-vug pore space are illustrated in figure 15.

Class 1 moldic searate-vug ooid grainstone	Class 1 intragrain microporous separate-vug ooid grainstone
Class 2 intrafossil seeparate-vug med xl grain-dominated dolopackstone	Class 3 grain mold seprate-vug fossil wackestone
Microporosity in an ooid (see arrow)	Class 1 intragrain microporous separate-vug ooid grainstone
Figure 15. Examples of separate-vug porosity

Separate vugs are not connected to each other. They are connected only through the interparticle pore space and, although the addition of separate vugs increases total porosity, it does not significantly increase permeability (Lucia 1983). Figure 16a illustrates this principle. Permeability of a moldic grainstone is less than would be expected if all the total porosity were interparticle and, at constant porosity, permeability increases with decreasing separate-vug porosity (Lucia and Conti 1987). The same is true for a large crystalline dolowackestone in that the data are plotted to the left of the class 1 field in proportion to the separate-vug porosity (Lucia 1983).

Figure 16. Cross plot illustrating the effect of separate-vug porosity on air permeability. (A) Grainstones with separate-vug porosity in the form of grain molds plot to the right of the grainstone field in proportion to the volume of separate-vug porosity. (B) Ooid grainstone with separate vugs in the form of intragranular microporosity plot to the right of the grainstone field.

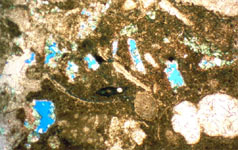
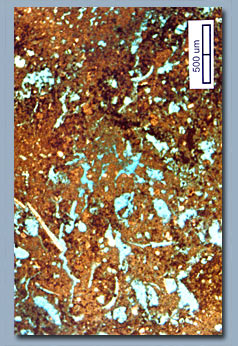
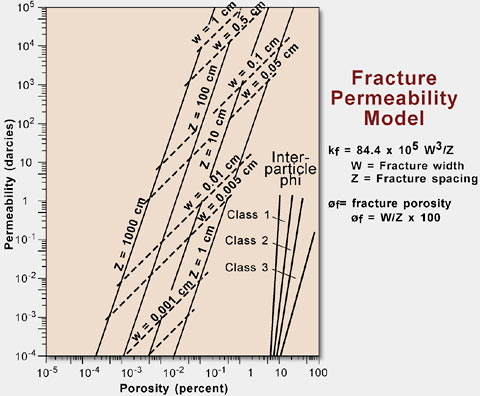
This principle is also true for intragrain microporosity. Fig. 16b shows data from a Cretaceous ooid grainstone from offshore Brazil with intragrain microporosity and intergrain pore space (Cruz, 1997). The plot shows that the permeability of the grainstone is less than would be expected if all the porosity were interparticle.

Petrophysics of Touching-Vug Pore Space

Examples of touching-vug pore types are illustrated in Fig. 17. Touching vugs can increase permeability well above what would be expected from the interparticle pore system and are usually considered to be filled with oil in reservoirs.

Cavernous touching-vug Niagarian (Silurian) Reef	Solution-enlarged fracture collapse breccia Ellenburger (Ordovician)
Crackle mosaic fracture Collapse breccia Ellenburger (Ordovician)	Collapse Breccia Ellenburger (Ordovician)
Dissolved anhydrite Grayburg (Permian)	Class 3 mud-dominated packstone with touching vugs of grain molds connected by microfractures
Figure 17. Examples of touching-vug pore types

Lucia (1983) illustrated this fact by comparing a plot of fracture permeability versus fracture porosity to the three permeability fields for interparticle porosity (Fig. 18).

Figure 18. Theoretical fracture air permeability-porosity relationship compared to the rock-fabric/petrophysical porosity, permeability fields (Lucia, 1983). W = fracture width, Z = fracture spacing.

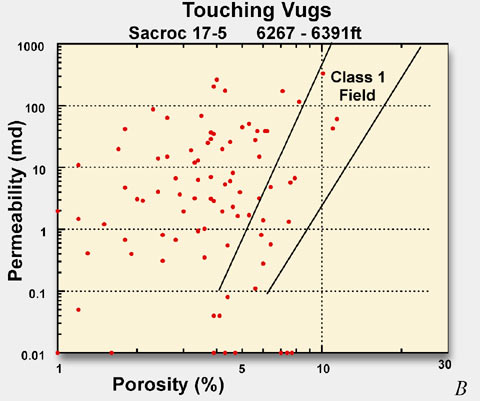
This graph shows that permeability in touching-vug pore systems has little relationship to porosity. Typical porosity-permeability cross plots from touching vugs have low (less than 6 percent) porosity and display unorganized scatter. An example is illustrated from a Pennsylvanian reservoir in West Texas (fig. 19).

Figure 19. Touching vug pore space from Sacroc field (Pennsylvanian), West Texas. (A) Photo of core slab and (B) porosity-permeability cross plot.